Materi Grafika Komputer Pertemuan Ke-6

ALGORITHMA GARIS

 Masalah : 
     Pixel mana yang harus dipilih untuk menggambar sebuah garis ?

 Algorithma garis adalah algorithma untuk menentukan lokasi pixel yang paling dekat dengan garis sebenarnya (actual line) 
 Ada tiga algorithma utama untuk menggambar garis : 
    Line Equation 
    DDA Algorithm 
    Bresenham’s Algorithm

Kuadran Garis

Di kuadran mana garis A ? 
Di kuadran mana garis B ? 
Dapatkah garis A dan B dinyatakan sebagai garis dengan kuadran yang sama ? 
Bagaimana caranya ? 
Bagaimana halnya dengan garis C dan D ?

 Garis A : (3 ; 1) – (8 ; 4) 
    Garis A berada di kuadran I 
 Garis B : (3 ; 7) – (1 ; 2) 
    Garis B berada di kuadran III 
    m = (2 – 7) / (1 – 3) = -5 / -2 = 2.5 
    tetapi apabila garis B dinyatakan sebagai (1 ; 2) – (3 ; 7) maka garis B akan berada di kuadran I 
    m = (7 – 2 ) / ( 3 – 1) = 5 / 2 = 2.5

LINE EQUATION 
 Sebuah garis lurus dapat diperoleh dengan menggunakan rumus : 
      y = mx + b 
 dimana : 
     m = gradien 
     b = perpotongan garis dengan sumbu y.

 Apabila dua pasang titik akhir dari sebuah garis dinyatakan sebagai (x1,y1) and (x2, y2), maka nilai dari gradien m dan lokasi b dapat dihitung dengan :

Contoh 

 Gambar garis (0,1) – (5,7) dengan menggunakan Line Equation

Gradien dan Tipe Garis

Tipe Garis

Dapatkah anda mencari perbedaan yang esensial antara garis A dan B (misal : gradien, pertambahan x dan y) ?

 Garis A : (3;1) – ( 8;4) 

    m = (y2 – y1) / (x2 – x1) = (4-1)/ (8-3) = 3/5= 0,6 m

    0 < m < 1 

    xi+1 = xi + 1 ; yi+1 = yi + d1 

 Garis B : (1;2) – (2;7) 

    m = (7-2) / (2-1) = 5 / 1 = 5 

    m > 1 

    xi+1 = xi + d2 ; yi+1 = yi + 1 

 Berapa nilai d1 dan d2 ? 

ALGORITHMA DDA 

 Digital differential analyzer (DDA) merupakan algorithma untuk menghitung posisi pixel disepanjang garis dengan menggunakan posisi pixel sebelumnya. 

 Algorithma berikut ini menggunakan asumsi bahwa garis berada di kuadran I atau II serta garis bertipe cenderung tegak atau cenderung mendatar.

 Untuk garis dengan 0 < m < 1, maka xi+1 = xi +1 dan :

 Untuk garis dengan m > 1, maka yi+1 = yi + 1 dan :

Algorithma DDA 

 Garis dengan 0 > m > -1, maka xi+1 = xi -1 dan

 Sedangkan bila m < -1, maka yi+1 = yi+1 dan

Contoh Algorithma DDA 

 Gambar garis dari (0;1) – (5;7) dengan menggunakan DDA. 

Algorithma Bresenham 

 Bresenham mengembangkan algorithma yang lebih efisien. 

 Algorithma ini mencari nilai integer yang paling mendekati garis sesungguhnya (actual line). 

 Algorithma ini tidak memerlukan pembagian.

 Algorithma Bresenham yang disajikan berikut ini hanya dapat digunakan untuk garis yang berada di kuadran I dan 0 < m < 1. 

 Anda yang ingin mempelajari pembuktian matematis dari algorithma Bresenham silahkan membaca buku Computer Graphics (Hearn dan Baker)

Algorithma Bresenham (0 < m < 1)

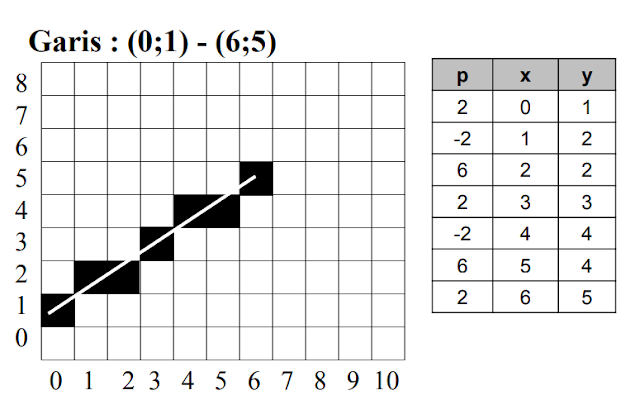
  Gambar garis berikut ini dengan menggunakan algorithma Bresenham : 

(0;1) – (6;5) 

(2;2) – (7;5) 

(0;1) – (5;7)

 Mengapa garis (0;1) – (5;7) tidak dapat digambar dengan tepat ? 

 Garis (0;1) – (5;7) mempunyai m = 1,2, dengan demikian asumsi pada algorithma tersebut tidak tepat dan harus disesuaikan.

Algorithma Bresenham ( m > 1)

Atribut Garis 

 Atribut garis meliputi : 

    Ketebalan garis

    Pola garis

    Warna garis