Materi Grafika Komputer Pertemuan Ke-11
ALGORITHMA CLIPPING
COHEN-SUTHERLAND
Clipping
Clipping adalah metoda untuk hanya
menampilkan garis pada area yang visible
(terlihat)
Visible dan Invisible Line
Berdasarkan posisi garis terhadap area
gambar maka garis dapat dibedakan menjadi
:
Bagaimana menentukan visible dan invisible
line?
fully visible : (x1 ≥ xmin) dan (x1 ≤ xmax)
dan (y1 ≥ ymin) dan (y1 ≤ ymax)
dan (x2 ≥ xmin) dan (x2 ≤ xmax)
dan (y2 ≥ ymin) dan (y2 ≤ ymax)
partially visible : -- coba sendiri dan anda akan
menemukan bahwa tidak mudah melakukan hal
tersebut ! --
Algorithma Clipping
Berbagai algorithma telah dikembangkan
untuk menangani masalah pemotongan garis
tersebut, antara lain :
Cyrus-Beck
Cohen-Sutherland
Algorithma Cohen-Sutherland
Area gambar dibatasi oleh xmin,xmax,
ymin,ymax
Cohen dan Sutherland memberikan kode
kepada tiap area yang mungkin dilewati oleh
sebuah garis atau disebut sebagai region
code.
T(op) = 1 jika ujung garis berada di atas area gambar selain itu 0 (nol)
B(ottom) = 1 jika ujung garis berada di bawah area gambar selain itu 0 (nol)
L(eft) = 1 jika ujung garis berada di kiri area gambar selain itu 0 (nol)
R(ight) = 1 jika ujung garis berada di kanan area gambar selain itu 0 (nol)
Sehingga diperoleh region code :
Garis kemungkinan partially visible atau fully invisible apabila
region code dari ujung garis tersebut mempunyai bit bernilai 1
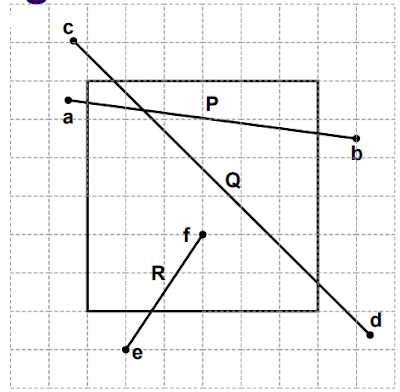
Region Code dari Pa = 0001
Region Code dari Pb = 0010
Region Code dari Qc = 1001
Region Code dari Qd = 0110
Region Code dari Re = 0100
Region Code dari Rf = 0000
Pemotongan (clipping) dilakukan terhadap
ujung-ujung garis yang region code berisi bit
bernilai 1.
Contoh sebelumnya menunjukkan bahwa
ujung Pa, Pb, Qc,Qd dan Re yang akan
mengalami pemotongan.
Ujung garis Pa
Region code Pa =1000
Pa berpotongan dengan garis
ymax sehingga menghasilkan
titik potong p1 (x1,ymax)
Ujung garis Pb
Region code Pb = 0010
Pb berpotongan dengan garis
xmax sehingga menghasilkan
titik potong p2 (xmax,y1)
Dengan menggunakan cara yang sama maka
lokasi titik potong untuk tiap area akan sesuai
tabel di bawah ini :
Koordinat titik potong dapat dicari dengan
cara :
Contoh
• Diketahui : area gambar : (1,2)-(5,5)
• Ditanyakan :
lokasi titik potong dari garis
P (2,1) - (4,6) terhadap area gambar
lokasi titik potong dari garis S (2,6) - (6,3)
m = (y2-y1) / (x2-x1)
= (6-1) / (4-2) = 5/2 =2,5
Ujung garis Pa
Region code Pa = 0100
Ujung Pa berpotongan dengan
garis ymin sehingga
p = x1+(ymin - y1) / m
p = 2 + (2 - 1) / 2,5 = 2,4
Jadi lokasi titik potong
p = (2,4;2)
Ujung garis Pb
Region code Pb = 1000
Ujung Pb berpotongan dengan
garis ymax sehingga
q = x1+(ymax - y1) / m
q = 2 + (5 - 1) / 2,5 = 3,6
Jadi lokasi titik potong
q = (3,6;5)
Dengan demikian garis P akan
di gambar dari p ke q atau dari
(2,4;2) menuju (3,6;5)
m = (y2-y1) / (x2-x1)
= (3-6) / (6-2) = -3/4 = -0,75
Ujung garis Sa
Region code Pa = 1000
Ujung Sa berpotongan dengan
garis ymax sehingga
p = x1+(ymax - y1) / m
p = 2 + (5 - 1) / -0,75 = 3,3
Jadi lokasi titik potong
p = (3,3;5)
Ujung garis Sb
Region code Sb = 0010
Ujung Sb berpotongan dengan
garis xmax sehingga
q = y1+ m * (xmax - x1)
q = 6 + (-0,75) * (5 - 2) = 3,75
Jadi lokasi titik potong
q = (5;3,75)
Dengan demikian garis S akan
di gambar dari p ke q atau dari
(3,3;5) menuju (5;3,75)
Untuk ujung-ujung garis dengan region code
berisi bit 1 maka ada tiga kemungkinan
perpotongan antara garis P dengan area
gambar
Apabila ditemukan lebih dari satu titik potong
maka pilih titik potong yang paling "dekat"
dengan area gambar.
Bagaimana pengertian "dekat" didefinisikan?
Tugas anda mendefinisikan pengertian "dekat"
tersebut!
Algorithma Cohen-Sutherland dapat dituliskan sebagai berikut :
Ambil ujung pertama (Pa) dari garis P
rc = Tentukan Region Code dari Pa
switch (rc)
0 : p = Pa
1 : p = (xmin,yp1)
2 : p = (xmax,yp2)
4 : p = (xp2,ymin)
5 : p1 = (xp2,ymin) ; p2 = (xmin,yp1)
= Tentukan mana yang lebih dekat antara p1 & p2
6 : p1 = (xp2,ymin) ; p2 = (xmax,yp2)
p
= Tentukan mana yang lebih dekat antara p1 & p2
8 : p = (xp1,ymax)
9 : p1 = (xp1,ymax) ; p2 = (xmin,yp1)
p
= Tentukan mana yang lebih dekat antara p1 & p2
10 : p1 = (xp2,ymax) ; p2 = (xmin,yp1)
p
= Tentukan mana yang lebih dekat antara p1 & p2
Ambil ujung kedua (Pb) dari garis P
rc = Tentukan Region Code dari Pb
switch (rc)
0 : q = Pb
1 : q = (xmin,yp1)
2 : q = (xmax,yp2)
4 : q = (xp2,ymin)
5 : p1 = (xp2,ymin) ; p2 = (xmin,yp1)
q
= Tentukan mana yang lebih dekat antara p1 & p2
6 : p1 = (xp2,ymin) ; p2 = (xmax,yp2)
q
= Tentukan mana yang lebih dekat antara p1 & p2
8 : p1 = (xp1,ymax)
9 : p1 = (xp1,ymax) ; p2 = (xmin,yp1)
q
= Tentukan mana yang lebih dekat antara p1 & p2
10 : p1 = (xp2,ymax) ; p2 = (xmin,yp1)
q
= Tentukan mana yang lebih dekat antara p1 & p2
Gambar garis dari p menuju q

























0 komentar: