MATERI LOGIKA DAN ALGORITMA PERTEMUAN KE-13

Penyelesaian Dengan Algoritma Pemrograman Greedy.

Algoritma GREEDY KNAPSACK. 
PROCEDURE GREEDY KNAPSACK ( W, x, n) 
float W[n], x[n], M, isi; 
Int i, n; 
x(1 : 1) < 0 ; isi < M ; 
FOR i < 1 TO n 
{ 
IF W[i] > M ; EXIT ENDIF 
x[i] < 1 
isi < isi – W[i] 
} 
IF i ≤ n ; x[i]  isi / W[i] ENDIF 
END_GREEDY KNAPSACK


Efektif jk data (Pi/Wi) disusun scr non decreasing dahulu. Penyelesaiannya : Dengan Algoritma Prg. Greedy. 

Diket. bhw kapasitas M = 20kg, dgn jmlh brg n=3 
Berat Wi masing2 brg = (W1, W2, W3) = (18, 15, 10) 
Nilai Pi masing2 brg = (P1, P2, P3) = (25, 24, 15) 
Lakuk’ p’urutan scr tdk naik thdp hasil Pi/Wi, misalnya : 

P1/Wi > 25/18 = 1,39 menjadi urutan ke 3 
P2/W2 > 24/15 = 1,60 menjadi urutan ke 1 
P3/W3 >15/10 = 1.50 menjadi urutan ke 2 
Sehingga m’hasilk’ pola urutan data yg baru,yaitu 
W1,W2,W3 > 15, 10, 18 dan P1,P2,P3 > 24, 15, 25

Lalu data2 tsb diinputk’ pd Alg. Greedy, terjadi proses : 

x(1:n) < 0 ; isi < 20 ; i = 1 
W(i) > isi ? > 15 > 20 ? > kondisi SALAH 
 x(1) = 1 > b’arti bhw brg tsb dpt dimuat seluruhnya. 
Isi = 20 - 15 >kapasitas ransel b’kurang dgn sisa 5kg i =2 
W(2) > isi ?? > 10 > 5 ?? > kondisi BENAR 
x(2)=5/10=1/2>benda 10kg hanya dpt dimuat 1/2 bgn yaitu 5 kg. 

i=3 
Endif > diakhiri krn ransel sdh penuh (max =20kg) 

Profit nilai yang didapat adalah : P1 + P2 + P3 yaitu: 
24.1+ 15.1/2 + 18.0 = 24 + 7.5 = 31.5

PROBLEMA DAN MODEL GRAPH DALAM METODE GREEDY ( Lanjutan ) 

1. TRAVELLING SALESMAN 
Untuk menentukan waktu perjalanan seorang salesman seminimal mungkin. 

Permasalahan: 
Setiap minggu sekali, seorang petugas kantor telepon berkeliling untuk mengumpulkan coin-coin pada telepon umum yang dipasang diberbagai tempat. Berangkat dari kantornya, ia mendatangi satu demi satu telepon umum tersebut dan akhirnya kembali ke kantor lagi. Masalahnya ia menginginkan suatu rute perjalanan dengan waktu minimal.


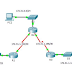
MODEL GRAPH :

Misalnya : Kantor pusat adalah simpul 1 dan misalnya ada 4 telepon umum, yg kita nyatakan sebagai simpul 2, 3, 4 dan 5 dan bilangan pada tiap-tiap ruas menunjukan waktu ( dalam menit ) perjalanan antara 2 simpul .

Langkah penyelesaian : 

1. Dimulai dari simpul yg diibaratkan sebagai kantor pusat yaitu simpul 1 . 

2.Dari simpul 1 pilih ruas yg memiliki waktu yg minimal. 

3. Lakukan terus pada simpul – simpul yg lainnya tepat satu kali yg nantinya Graph akan membentuk Graph tertutup karena perjalanan akan kembali ke kantor pusat. 

4. Problema diatas menghasilkan waktu minimalnya adalah 45 menit dan diperoleh perjalanan sbb :

Problema diatas menghasilkan waktu minimalnya adalah 45 menit dan diperoleh perjalanan sbb :

2. MINIMUM SPANNING TREE 

Kasus MST Problem = m’cari min.biaya (cost) spanning tree dr setiap ruas (edge) graph yg m’btk pohon (tree). Solusi dr p’masalah’ ini : 

a. Dgn memilih ruas suatu graph yg memenuhi kriteria dr optimisasi yg m’hasilk’ biaya min. 

b. Penambah’ dr setiap ruas pd seluruh ruas yg m’btk graph akan m’hasilk’ nilai/biaya yg kecil (minimum cost). 

Kriteria2 dr spanning tree, yakni : 

1. Setiap ruas pada graph harus terhubung (conected) 

2. Setiap ruas pd graph hrs mpy nilai (label graph) 

3. Setiap ruas pd graph tdk mpy arah (graph tdk berarah)

Proses Total minimum cost terbentuknya graph dgn tahapan sbb: 

• Dari graph yg tetbentuk, apakah memenuhi kriteria MST. 

• Lakukan secara urut dr simpul ruas awal s/d ruas akhir 

• Pada setiap simpul ruas perhatikan nilai/cost dr tiap-tiap ruas 

• Ambil nilai yg paling kecil (jarak tertpendek setiap ruas). 

• Lanjutkan s/d semua simpul ruas tergambar pd spanning tree 

• Jumlahkan nilai/cost yg dipilih tadi.

3. SHORTEST PATH PROBLEM 

Permasalahan : menghitung jalur terpendek dr sbh graph berarah. 

Kriteria utk permasalahan jalur terpendek/SP problem tsb : 

1. Setiap ruas pd graph hrs mpy nilai (label graph) 

2. Setiap ruas pd graph tdk hrs terhubung (unconnected) 

3. Setiap ruas pd graph tsb hrs mempunyai arah (graph berarah).