MATERI LOGIKA DAN ALGORITMA PERTEMUAN KE-14

PROBLEMA DAN MODEL GRAPH DALAM METODE GREEDY

1. PEWARNAAN ( COLORING ) Problema pemberian warna kepada semua simpul, sedemikian sehingga 2 simpul yang berdampingan ( ada ruas menghubungkan ke dua simpul tersebut ) mempunyai warna yang berbeda .Banyak warna yang dipergunkan , diminta seminimal mungkin

Contoh :

Permasalahan : 

Menentukan pola lampu lalulintas dengan jumlah fase minimal, dan pada setiap fase tidak ada perjalanan yang saling melintas . Perjalanan yang diperbolehkan adalah : A ke B, A ke C, A ke D, B ke C, B ke D, E ke B, E ke C dan E ke D

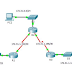
Langkah-langkah penyelesaian masalah : 

1. Tentukan simpul dari perjalanan yang diperbolehkan ( untuk peletakan simpulnya bebas ) 

2.Tentukan ruas untuk menghubungkan 2 simpul yg menyatakan 2 perjalanan yg saling melintas

3. Beri warna pada setiap simpul dengan warna warna baru. 

- Bila Simpul berdampingan maka berilah warna lain. 

- Bila simpul tidak bedampingan maka berilah warna yang sama 

4. Kita lihat Bahwa simpul AB , BC dan ED tidak dihubungkan oleh suatu ruas jadi untuk simpul tersebut tidak pernah melintas perjalanan-perjalanan lain dan simpul tersebut selalu berlaku lampu hijau 

5. Tentukan pembagian masing –masing simpul yang sudah diberikan warna. 

Putih = ( AC, AD ) 

Hitam = ( BD, EB ) 

Merah = ( EC )

Catatan :

 Pembagian simpul berdasarkan simpul yang tidak langsung berhubungan seminimal mungkin ( BISA DILAKUKAN DENGAN BEBERAPA KEMUNGKINAN ) 

 6. Dari langkah ke 5 diperoleh 3 fase, sehingga bisa kita simpulkan keseluruhan situasi dan hasilnya dapat dinyatakan dengan :